KickStart 2019 Round D Question A. X or What

Posted on | In |

See here.

Problem

Steven has an array of N non-negative integers. The i-th integer (indexed starting from 0) in the array is Ai.

Steven really likes sub-intervals of A that are xor-even. Formally, a sub-interval of A is a pair of indices (L, R), denoting the elements . The xor-sum of this sub-interval is xor xor ... xor xor , where xor is the bitwise exclusive or.

A sub-interval is xor-even if its xor-sum has an even number of set bits in its binary representation.

Steven would like to make Q modifications to the array. The i-th modification changes the $P_i$-th (indexed from 0) element to $V_i$. Steven would like to know, what is the size of the xor-even sub-interval of A with the most elements after each modification?

Input

The first line of the input gives the number of test cases, T. T test cases follow.

Each test case starts with a line containing two integers N and Q, denoting the number of elements in Steven's array and the number of modifications, respectively.

The second line contains N integers. The i-th of them gives $A_i$ indicating the i-th integer in Steven's array.

Then, Q lines follow, describing the modifications. The i-th line contains $P_i$ and $V_i$, The i-th modification changes the $P_i$-th element to $V_i$. indicating that the i-th modification changes the $P_i$-th (indexed from 0) element to $V_i$.

Output

For each test case, output one line containing Case #x: y_1 y_2 ... y_Q, where x is the test case number (starting from 1) and y_i is the number of elements in the largest xor-even sub-interval of A after the i-th modification. If there are no xor-even sub-intervals, then output 0.

Sample Input and Output

Input

1
2
3
4
5
6
7
8
9
2
4 3
10 21 3 7
1 13
0 32
2 22
5 1
14 1 15 20 26
4 26

Output

1
2
Case #1: 4 3 4
Case #2: 4

Solution

This is a problem that we can tear it apart into two sub-problems, how to determine if a number has even or odd 1s in its bits, and how to find the longest subarray. Let's do it one by one.

How to determine if a number has even or odd 1s in its bits?

This one looks simple, while it can also be pretty tricky. Let's start from the most naive one.

Naive

Naively compare every bits and count them, see if there's even of them.

1
2
3
4
5
6
7
8
9
10
boolean evenOnes(int n) {
  int count = 0;
  while (n != 0) {
    if ((n & 1) == 1) {
      count++;
    }
    n >>= 1;
  }
  return (count & 1) == 0;
}

A small improve

We have noticed that this require $k$ times of comparisons, while $k$ denotes the number of bits of the integer. In Java 8, $k = 32$.

Can we improve it a little bit? Here a method that allow us to compare exactly $a$ times, while $a$ denotes the total number of 1 in $n$'s bits presentation. Here's how we do it:

1
2
3
4
5
6
7
8
boolean evenOnes(int n) {
  int count = 0;
  while (n!=0) {
    n &= n-1;
    count++;
  }
  return (count & 1) == 0;
}

How did this work? Take a look at the figure.

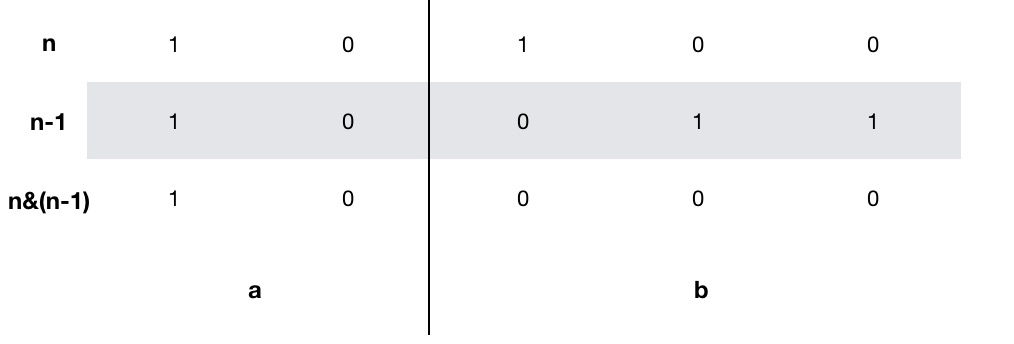
Figure 1

Say we split the binary representation of the integer n into two parts, b denotes from the first 1 to the lowest bit, and a for the rest.

For $n-1$, we can see that a part stayed the same and every bits get flipped in b part, thus the & operation between will keep everything in a the same, and turn every bits in b into 0. As a result, we erased the first 1 in $n$, from the lowest bit to highest. The loop terminates until $n = 0$, which indicates that all 1 have been erased from $n$. Counting the time of the loop, would be the number of 1s in n.

Can we do even better?

Yes we can, but to be strictly correct, we cannot actually call this better under all circumstance (Imagine if the n is 0, can we actually do it any better?). The fact is we can do this by do five comparison under all circumstance, thus for any $n$ that has more than five 1s, it's better, other than that, it's actually worse.

But we're presenting the method anyway, because, firstly, the method is tricky and interesting, and secondly, in practice, this method is stable, especially for input that has a lot of 1, it's much faster.

Here's the code, and it's pretty simple.

1
2
3
4
5
6
7
8
boolean evenOnes(int x) {
  x ^= x >> 1;
  x ^= x >> 2;
  x ^= x >> 4;
  x ^= x >> 8;
  x ^= x >> 16;
  return (x&1) == 0;
}

Now, here's the tricky part, let's start from the first comparison: x ^= x >> 1

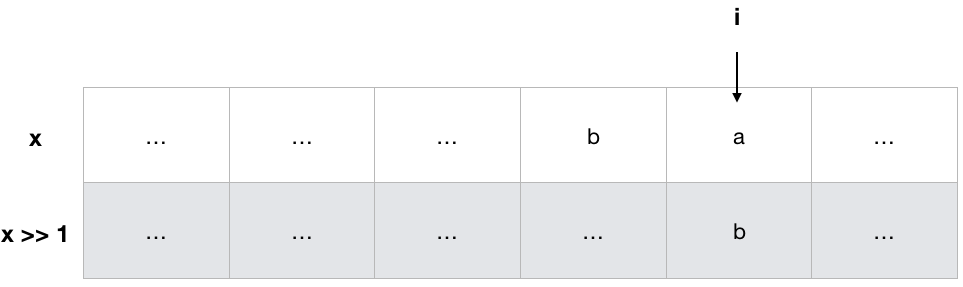
Figure 2

See from the figure, and concentrate on the i-th bit. Under what circumstance would the i-th bit be 1 ? The answer is there's only one 1 at the i-th and (i+1)-th bit in x. Which means, if the result bit at the i-th bit is 1, that indicates there are odd number of 1s between the i-th and the (i+1)-th bits, and vice versa.

Now let's take a look at the second comparison: x ^= x >> 2;, which can be indicated by the figure below:

Figure 2

Now remember the x is the x after the first comparison, which means the i-th bit, a indicates whether there're odd number of 1 in the i-th and (i+1)-th bits in the original input, and for b, it indicates whether there're odd number of 1 in the (i+2)-th and (i+3)-th bits.

Now let's see what would happen after this comparison. Consider this: What would a and b like, if we want the i-th bit is 1 after the operation? The only answer is that, only one out of a and b is 1. Recall that a and b indicates the oddness of the original input on there representing range, and only one of them have odd 1s. So if we merge the two ranges, the new range would have odd 1s in it. Thus we could say, the bit on i-th position indicates the oddness of 1s from i-th position to (i+3)-th position in the original input.

The same things goes all the way to the range is length 32, the number of bits of an integer in Java 8. Then we can say: The bit at the 0-th position indicates the oddness of 1 for the range from 0 to 31, which is the total input.

Now we have solved our first problem, let's see the second.

Find the Longest Sub-array that Every Element Has Even 1's.

Here, Even means odd-even even, not an "equal" even.

The brute-force way, of course, it after each modification, go through all the sub-arrays and record the longest one. This is a $O(n^2)$ algorithms and too trivial that we don't actually need to discuss more about it.

In order to improve it, we have noticed an interesting fact: For any a & b = x, the x would have odd 1's if and only if one of a and b have odd 1's. Prove it as an exercise, it's not hard!

So here are two conditions: the number of odd-1's element in the array is even, and the number is odd. Things are pretty easy for the even situation: the longest sub-array is the whole array. For the odd situation, the longest sub-array is one of the following sub-arrays: the subarray right after the first odd-1's element to the end, and the subarray from the beginning to the element right before the last odd-1's element.

To avoid looking for the first and last odd-1's element after every modifications, we can use a sorted set to record the positions of them, thus we only need to add or remove one element to the set, or do nothing in each modification. The time complexity is $O(log(k))$ for each modification, where $k$ indicates the size of the set.

Here's an implementation of it:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public List<Integer> solve(int n, int q, int[] nums, int[][] modis) {
  List<Integer> ans = new ArrayList<>();
  TreeSet<Integer> positions = new TreeSet<>();
  for (int i=0; i<n; i++) {
      if (!evenOnes(nums[i])) {
          positions.add(i);
      }
  }

  for (int[] modi: modis) {
      int pos = modi[0];
      int val = modi[1];
      if (evenOnes(val)) {
          if (positions.contains(pos)) {
              positions.remove(pos);
          }
      } else {
          if (!positions.contains(pos)) {
              positions.add(pos);
          }
      }

      if ((positions.size() & 1) == 0) {
          ans.add(n);
      } else {
          ans.add(Math.max(n - positions.first() - 1, positions.last()));
      }
  }

  return ans;
}

In total, the time complexity of the algorithm is $O((k+q)log(k))$, where $k$ denotes the size of the set, and $q$ is the number of queries.

It's also mentioned that van Emde Boas trees can solve this problem, but I'll leave it to another separate article to talk about it, for this one is already long enough.